Introduction

Building a super fast sudoku solving algorithm is pretty difficult, however there are a lot of smart decisions one can consider while contructing a sudoku solving algorithm. Today we will create one using Javascript.

Sudoku Rules

The sudoku game rules are very simple and straight forward, it follows these simple rules:

1. The same number must not repeat horizontally
2. The same number must not repeat vertically
3. The same number must not repeat in a square

There are of course other rules such as each puzzle must have only one unique solution or self made rules however these won't be discussed as they are not relevant.

For example the number 5

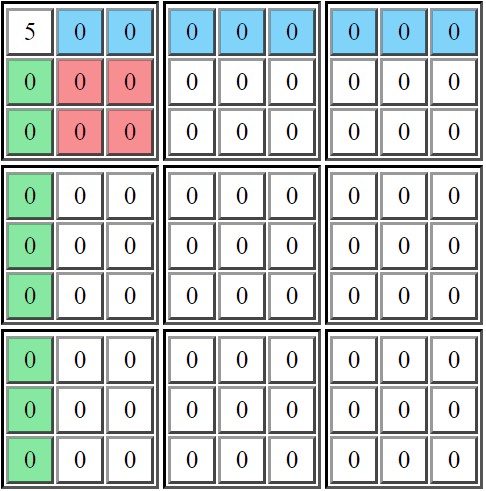
As we can see here the green, red and blue lines are the tiles where we can't put another 5. This is important because we can use these constraints to lessen the computation the computer has to do.

How the algorithm works

The way the algorithm works is simple, we minimize the computation the computer has to do by putting constraints based on traditional sudoku rules and without the use of a brute-force algorithm that checks every possibility.

I would like you to imagine an empty sudoku board like this:

0 0 0 | 0 0 0 | 0 0 0
0 0 0 | 0 0 0 | 0 0 0
0 0 0 | 0 0 0 | 0 0 0 
------+------+------
0 0 0 | 0 0 0 | 0 0 0
0 0 0 | 0 0 0 | 0 0 0
0 0 0 | 0 0 0 | 0 0 0 
------+------+------
0 0 0 | 0 0 0 | 0 0 0
0 0 0 | 0 0 0 | 0 0 0
0 0 0 | 0 0 0 | 0 0 0 

Now consider the rules we already know, if there is absolutely no number in any tile it means every thing from 1 to 9 can be inserted in every tile, like this:

123456789 123456789 123456789 | 123456789 123456789 123456789 | 123456789 123456789 123456789
123456789 123456789 123456789 | 123456789 123456789 123456789 | 123456789 123456789 123456789
123456789 123456789 123456789 | 123456789 123456789 123456789 | 123456789 123456789 123456789
------------------------------+-------------------------------+------------------------------
123456789 123456789 123456789 | 123456789 123456789 123456789 | 123456789 123456789 123456789
123456789 123456789 123456789 | 123456789 123456789 123456789 | 123456789 123456789 123456789
123456789 123456789 123456789 | 123456789 123456789 123456789 | 123456789 123456789 123456789
------------------------------+-------------------------------+------------------------------
123456789 123456789 123456789 | 123456789 123456789 123456789 | 123456789 123456789 123456789
123456789 123456789 123456789 | 123456789 123456789 123456789 | 123456789 123456789 123456789
123456789 123456789 123456789 | 123456789 123456789 123456789 | 123456789 123456789 123456789

We can use this full board to solve our sudoku puzzles!

Checking and removing

So let's consider this puzzle as an example:

0 0 0 | 0 0 4 | 0 0 0
0 0 5 | 0 0 0 | 0 0 0
0 0 0 | 0 0 0 | 0 0 0 
------+------+------
0 0 0 | 0 6 0 | 0 0 0
0 0 0 | 0 0 0 | 0 5 0
0 0 0 | 0 0 0 | 0 0 0 
------+------+------
0 0 0 | 0 5 0 | 0 0 0
0 0 0 | 0 0 0 | 0 0 0
0 0 0 | 0 0 0 | 0 0 0 

Now let's insert the above sudoku puzzle into the board that contains every possibility.

123456789 123456789 123456789 | 123456789 123456789     4     | 123456789 123456789 123456789
123456789 123456789     5     | 123456789 123456789 123456789 | 123456789 123456789 123456789
123456789 123456789 123456789 | 123456789 123456789 123456789 | 123456789 123456789 123456789
------------------------------+-------------------------------+------------------------------
123456789 123456789 123456789 | 123456789      6    123456789 | 123456789 123456789 123456789
123456789 123456789 123456789 | 123456789 123456789 123456789 | 123456789     5     123456789
123456789 123456789 123456789 | 123456789 123456789 123456789 | 123456789 123456789 123456789
------------------------------+-------------------------------+------------------------------
123456789 123456789 123456789 | 123456789 123456789 123456789 | 123456789 123456789 123456789
123456789 123456789 123456789 | 123456789     5     123456789 | 123456789 123456789 123456789
123456789 123456789 123456789 | 123456789 123456789 123456789 | 123456789 123456789 123456789

Based on traditional sudoku rules, we can eliminate what we can't put into each vertical, horizontal, and same-square tiles.

1236789 1236789 1236789      | 12356789 123789    4     | 12356789 1236789 12356789
12346789 12346789 5          | 1236789  123789  1236789 | 12346789 12346789 12346789
12346789 12346789 12346789   | 12356789 123789 12356789 | 123456789 12346789 123456789 
-----------------------------+--------------------------+------------------------------
12345789 12345789 1234789    | 12345789    6   1235789  | 1234789   1234789 1234789
12346789 12346789 12346789   | 1234789 1234789 123789   | 12346789     5    12346789
123456789 123456789 12346789 | 12345789 1234789 1235789 | 12346789 12346789 12346789 
-----------------------------+--------------------------+------------------------------
12346789 12346789 12346789   | 12346789    5    1236789 | 1346789 12346789   12346789
123456789 123456789 12346789 | 12346789 1234789 1236789 | 123456789 12346789 123456789
123456789 123456789 12346789 | 12346789 1234789 1236789 | 123456789 12346789 123456789 

NOTE: The numbers in each tile are the possibilities you can insert in that specific tile

By doing this process we have shaved off a huge chunk of computational power and options that can be inserted into each specific tile. However this is not enough, this hasn't solved the puzzle completely just lowered the possibilities. Let's explain the next step in the algorithm.

Searching and inserting

The second part of the algorithm is a bit more complicated because we will have to use a recursive depth-first searching algorithm, however that does not mean it's more complicated code wise, just logic wise.

Understanding depth-first searching

Depth-first searching can be explained in a very simple way. Take this visualization of a tree graph below, imagine there is a hidden gold coin in the numbers (4, 5, 6, 7, 10, 11) but we don't know which one and our goal is to find it.

The way depth-first searching works is we take the first arbitrary branching from our starting node (the number 1) and dive deep into it. For example:

1. Start from node 1 is the gold coin here? If yes end program, if not continue searching
2. Dive into the next adjacent branch/node that is selected arbitrary
3. Does the node number 2 have a gold coin? If yes end program, if not continue searching
4. Does the node number 3 have a gold coin? If yes end program, if not continue searching

NOTE: As you can see we're diving deeper and deeper into the same branch.

5. Does the node number 4 have a gold coin? If yes end program, if not then backtrack to node number 3 because we can't go any deeper (node 4 doesn't have any adjacent nodes except the one we came from)
6. Does the node number 5 have a gold coin? If yes end program, if not then backtrack to node number 3 because we can't go any deeper (node 5 doesn't have any adjacent nodes except the one we came from)
7. We have explored all of node 3 and found nothing so we backtrack again back to node number 2 and explore the other option (node number 6)
8. Does the node number 6 have a gold coin? If yes end program, if not then backtrack to node number 2 because we can't go any deeper (node 6 doesn't have any adjacent nodes except the one we came from)
9. We have explored all of node 2 and found nothing so we backtrack again back to node number 1 and explore the other options

Continue and repeat this process for every branch or node adjacent to the starting node until the gold coin is found. The only difference in this context is instead of a gold coin we will be searching for a "solved" sudoku board.

What happens in each branch

What happens in each branch is this:

1. Find the first field that has more than 1 possibility
2. Assign first available number to the tile and run the elimination process vertically, horizontally, and in same-square tiles
3. Does it lead to an incorrectly solved puzzle or a contradiction? If so the solved sudoku is not on this branch. Terminate and backtrack to before making this choice and take the other choice
4. Does it lead to a correct solved puzzle? that branch will return the solved board

Starting at top left corner let's insert the first possibility (1) into the tile.

    1   1236789 1236789      | 12356789 123789    4     | 12356789 1236789 12356789
12346789 12346789 5          | 1236789  123789  1236789 | 12346789 12346789 12346789
12346789 12346789 12346789   | 12356789 123789 12356789 | 123456789 12346789 123456789 
-----------------------------+--------------------------+------------------------------
12345789 12345789 1234789    | 12345789    6   1235789  | 1234789   1234789 1234789
12346789 12346789 12346789   | 1234789 1234789 123789   | 12346789     5    12346789
123456789 123456789 12346789 | 12345789 1234789 1235789 | 12346789 12346789 12346789 
-----------------------------+--------------------------+------------------------------
12346789 12346789 12346789   | 12346789    5    1236789 | 1346789 12346789   12346789
123456789 123456789 12346789 | 12346789 1234789 1236789 | 123456789 12346789 123456789
123456789 123456789 12346789 | 12346789 1234789 1236789 | 123456789 12346789 123456789 

The trickling effect of removing 1 from every vertical, horizontal and same-square tile starts

    1    236789  236789      |  2356789  23789    4     |  2356789  236789  2356789
 2346789   2346789 5         | 1236789  123789  1236789 | 12346789 12346789 12346789
 2346789  2346789  2346789   | 12356789 123789 12356789 | 123456789 12346789 123456789 
-----------------------------+--------------------------+------------------------------
 2345789 12345789 1234789    | 12345789    6   1235789  | 1234789   1234789 1234789
 2346789 12346789 12346789   | 1234789 1234789 123789   | 12346789     5    12346789
 23456789 123456789 12346789 | 12345789 1234789 1235789 | 12346789 12346789 12346789 
-----------------------------+--------------------------+------------------------------
 2346789 12346789 12346789   | 12346789    5    1236789 | 1346789 12346789   12346789
 23456789 123456789 12346789 | 12346789 1234789 1236789 | 123456789 12346789 123456789
 23456789 123456789 12346789 | 12346789 1234789 1236789 | 123456789 12346789 123456789 

We have eliminated a lot of possibilities. Let's go to the second top-most tile and insert the first option (2) then trigger the trickling effect again.

    1       2      36789    |  356789    3789    4     |  356789   36789    356789
 346789   346789    5       | 1236789  123789  1236789 | 12346789 12346789 12346789
 346789   346789   346789   | 12356789 123789 12356789 | 123456789 12346789 123456789 
----------------------------+--------------------------+------------------------------
 2345789  1345789 1234789    | 12345789    6   1235789  | 1234789   1234789 1234789
 2346789  1346789 12346789   | 1234789 1234789 123789   | 12346789     5    12346789
 23456789 13456789 12346789  | 12345789 1234789 1235789 | 12346789 12346789 12346789 
-----------------------------+--------------------------+------------------------------
 2346789   1346789 12346789  | 12346789    5    1236789 | 1346789 12346789   12346789
 23456789  13456789 12346789 | 12346789 1234789 1236789 | 123456789 12346789 123456789
 23456789  13456789 12346789 | 12346789 1234789 1236789 | 123456789 12346789 123456789 

We have eliminated a lot of possibilities again. Now let's continue this until we do the whole top-most row.

  1       2       3         |  5        7     4         |  6       8    9
 46789   46789    5         | 123689  12389  123689     | 123478 12347 12347
 46789   46789   46789      | 123689 12389   123689     | 123478 12347 1234579
----------------------------+--------------------------+------------------------------
 2345789  1345789 124789    | 1234789    6   1235789    | 1234789   123479 123478
 2346789  1346789 1246789   | 1234789 123489 123789     | 1234789     5    1234678
 23456789 13456789 1246789  | 1234789 123489 1235789    | 1234789 1234679 1234678
-----------------------------+--------------------------+-----------------------------
 2346789   1346789 1246789  | 12346789    5    1236789  | 134789 12346789   1234678
 23456789  13456789 1246789 | 12346789 123489 1236789   | 12345789 12346789 12345678
 23456789  13456789 1246789 | 12346789 123489 1236789   | 12345789 12346789 12345678

We continue this process until we reach the end (assuming we have made every right decision) the sudoku puzzle will be solved and look like the board below, however if at any point we reach a contradiction or unsolved state we will terminate the branch and backtrack.

1 2 3 | 5 7 4 | 6 8 9
4 6 5 | 1 8 9 | 2 3 7
7 8 9 | 2 3 6 | 1 4 5 
------+------+-------
2 1 4 | 3 6 5 | 7 9 8
3 7 6 | 8 9 1 | 4 5 2
5 9 8 | 4 2 7 | 3 1 6 
------+------+-------
6 3 1 | 7 5 8 | 9 2 4
8 4 7 | 9 1 2 | 5 6 3
9 5 2 | 6 4 3 | 8 7 1 

You should have noticed by now that the solved sudoku top-most and second row has the pattern of the algorithm we discussed above. Now let's program it!

Programming it

First off let's try to imagine what data structure can represent a sudoku board in a programming language. The first instinct is going to be a 2D-array which is not a terrible idea but it wouldn't work in our case since we want to easily index and look up vertical, horizontal, and same-square tiles. Therefor we have to go a step further and program a data structure that can:

• Represent each individual tile
• Represent each horizontal sequence
• Represent each vertical sequence
• Represent each same-square tile
• Keep track of each tile and its associated vertical, horizontal, and same-square tiles

NOTE: We can give each tile on a sudoku board a name by using the numbers 1 to 9 and the letters A to I, something like this:

 A1 A2 A3| A4 A5 A6| A7 A8 A9
 B1 B2 B3| B4 B5 B6| B7 B8 B9
 C1 C2 C3| C4 C5 C6| C7 C8 C9
---------+---------+---------
 D1 D2 D3| D4 D5 D6| D7 D8 D9
 E1 E2 E3| E4 E5 E6| E7 E8 E9
 F1 F2 F3| F4 F5 F6| F7 F8 F9
---------+---------+---------
 G1 G2 G3| G4 G5 G6| G7 G8 G9
 H1 H2 H3| H4 H5 H6| H7 H8 H9
 I1 I2 I3| I4 I5 I6| I7 I8 I9

Setting up a system for look up and indexing

let's start by making a file called solver.js (you can name it whatever else you would like) and add a class containing these properties to it.

class Solver {
    constructor() {
    // the possibilities each tile can have
    this.digits = '123456789';
    // the tiles letter names
    this.rows = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I'];
    // the tiles number names
    this.cols = ['1', '2', '3', '4', '5', '6', '7', '8', '9'];
    // every 3 rows letter names
    this.rRows = [['A', 'B', 'C'], ['D', 'E', 'F'], ['G', 'H', 'I']];
    // every 3 rows number names
    this.cCols = [[1, 2, 3], [4, 5, 6], [7, 8, 9]];
    // all these will be filled for easier look up
    this.verticalUnits = [];
    this.horizontalUnits = [];
    this.squarePeers = [];
    this.units = {};
    this.peers = {};
    this.filledBoard = {};

    this.squares = this.cross(this.rows, this.cols);
    this.initializeBoard();
    }
}

We will fill up the empty arrays and objects above so we can search through each sequence faster. Cross and initializeBoard are two functions that bring together all the pieces to build the structure for our algorithm. Let's look further at the cross function.

cross(X, Y) {
    const tempArr = [];
    for (const x of X) {
      for (const y of Y) {
        tempArr.push(x + y);
      }
    }
    return tempArr;
}

The cross function does a very simple operation. It takes every item inside two arrays and adds them together so in the case of:

this.squares = this.cross(this.rows, this.cols);

we will have A1, A2, A3, A4... then B1, B2, B3... So every possible combination the board can have.

Let's have a look at the initializeBoard function.

initializeBoard() {
  for (const c of this.cols) {
    this.verticalUnits.push(this.cross(this.rows, c));
  }

  for (const r of this.rows) {
    this.horizontalUnits.push(this.cross(r, this.cols));
  }

  for (const rs of this.rRows) {
    for (const cs of this.cCols) {
      this.squarePeers.push(this.cross(rs, cs));
    }
  }
  // for each tile create a key that contains all its associated
  // vertical, horizontal, and 
  // same-square associated tiles as value
  for (const s of this.squares) {
    this.units[s] = [];
    
    for (const vu of this.verticalUnits) {
      if (vu.includes(s)) {
        this.units[s].push(vu);
        }
    }

    for (const hu of this.horizontalUnits) {
      if (hu.includes(s)) {
        this.units[s].push(hu)
      }
    }

    for (const sqp of this.squarePeers) {
      if (sqp.includes(s)) {
        this.units[s].push(sqp);
      }
    }
  }
  
  for (const s of this.squares) {
    this.peers[s] = [];
    for (const u of this.units[s]) {
      for (const s2 of u) {
        if (s2 !== s) {
          this.peers[s].push(s2);
        }
      }
    }
  }

  // fill a board object with each tile name as key
  // and number from 1 to 9 as value
  for (const s of this.squares) {
    his.filledBoard[s] = this.digits;
  }
}

Explanation for pieces of the code:

• Line 2-4: Create an array with each individual tile and its associated vertical tiles, using *2 as an example:

00 A2 00 | 00 00 00 | 00 00 00
00 B2 00 | 00 00 00 | 00 00 00
00 C2 00 | 00 00 00 | 00 00 00 
---------+----------+---------
00 D2 00 | 00 00 00 | 00 00 00
00 E2 00 | 00 00 00 | 00 00 00
00 F2 00 | 00 00 00 | 00 00 00
---------+----------+---------
00 G2 00 | 00 00 00 | 00 00 00
00 H2 00 | 00 00 00 | 00 00 00
00 I2 00 | 00 00 00 | 00 00 00 

• Line 6-8: Create an array with each individual tile and its associated horizontal tiles, using C* as an example:

00 00 00 | 00 00 00 | 00 00 00
00 00 00 | 00 00 00 | 00 00 00
C1 C2 C3 | C4 C5 C6 | C7 C8 C9 
---------+----------+---------
00 00 00 | 00 00 00 | 00 00 00
00 00 00 | 00 00 00 | 00 00 00
00 00 00 | 00 00 00 | 00 00 00
---------+----------+---------
00 00 00 | 00 00 00 | 00 00 00
00 00 00 | 00 00 00 | 00 00 00
00 00 00 | 00 00 00 | 00 00 00

• Line 10-14: Create an array for a tiles associated square, using ABC* as an example:

A1 A2 A3 | 00 00 00 | 00 00 00
B1 B2 B3 | 00 00 00 | 00 00 00
C1 C2 C3 | 00 00 00 | 00 00 00
---------+----------+---------
00 00 00 | 00 00 00 | 00 00 00
00 00 00 | 00 00 00 | 00 00 00
00 00 00 | 00 00 00 | 00 00 00
---------+----------+---------
00 00 00 | 00 00 00 | 00 00 00
00 00 00 | 00 00 00 | 00 00 00
00 00 00 | 00 00 00 | 00 00 00

• Line 40-49: Creates a key/value pair with each tile as key and all its associated vertical, horizontal, and same-square tiles (itself not included) as value, using C2 as an example:

A1 A2 A3 | 00 00 00 | 00 00 00
B1 B2 B3 | 00 00 00 | 00 00 00
C1 00 C3 | C4 C5 C6 | C7 C8 C9 
---------+----------+---------
00 D2 00 | 00 00 00 | 00 00 00
00 E2 00 | 00 00 00 | 00 00 00
00 F2 00 | 00 00 00 | 00 00 00
---------+----------+---------
00 G2 00 | 00 00 00 | 00 00 00
00 H2 00 | 00 00 00 | 00 00 00
00 I2 00 | 00 00 00 | 00 00 00

The function puts together all the pieces by constructing all the necessary associated tiles. The function also fills in the "filledBoard" object that has each tile as key (like the board above) and the numbers 1-9 as value.

Now we have set up a system where we can easily index and look up each tile and it's associated tiles. Let's write the algorithm functions.

Solving the sudoku puzzle

It's important to establish how we read the sudoku puzzle that is being solved. First instinct would be a 2D array, but that would make it very inconvenient. Therefore we will take the given sudoku puzzle as a string which means every part of the board will go in a chronological order.

For example:

0 0 0 | 0 0 4 | 0 0 0
0 0 5 | 0 0 0 | 0 0 0
0 0 0 | 0 0 0 | 0 0 0 
------+------+------
0 0 0 | 0 6 0 | 0 0 0
0 0 0 | 0 0 0 | 0 5 0
0 0 0 | 0 0 0 | 0 0 0 
------+------+------
0 0 0 | 0 5 0 | 0 0 0
0 0 0 | 0 0 0 | 0 0 0
0 0 0 | 0 0 0 | 0 0 0 

Would become:

000004000005000000000060000000000050000050000000000000000000000

Now that it's established, let's move on to the first part of the code.

Taking in the puzzle as input

solve(grid) {
  // create local copy of the filled board
  const board = { ...this.filledBoard }

  for (let i = 0; i < this.squares.length; i++) {
    if (this.digits.includes(grid[i]) && !this.assign(board, this.squares[i], grid[i])) {
      return false;
    }
  }

  return board;
}

The solve function places the numbers from the given puzzle board on the filledBoard local copy. Then eliminate the numbers vertically, horizontally, and in same-square.

NOTE: If the character is 0 we skip without executing the assign function due to the way the AND operator works.

Lets check the assign function next.

Assigning the puzzle position onto the grid

assign(board, tile, digit) {
  // get all the contents of the tile
  const tileValues = board[tile];
  let result = true;
  // eliminate the contents one by one as long as they aren't the digit
  for (let i = 0; i < tileValues.length; i++) {
    if (tileValues[i] !== digit) {
      result = this.eliminate(board, tile, tileValues[i]);
      }
  }
  return (result ? board : false);
}

The assign function gets the contents of the tile then eliminates the contents of the tile that are not the same digit as on the given puzzle. Let's take a look at the first top-most level corner of our puzzle as an example:

0 0 0 |
0 0 5 |
0 0 0 |

We have to insert the 5.

123456789 123456789 123456789 |
123456789 123456789 123456789 |
123456789 123456789 123456789 |

Eliminate the numbers and make it become:

12346789 12346789 12346789 |
12346789 12346789     5    |
12346789 12346789 12346789 |

The eliminate function takes care of eliminating it in associated tiles. Let's go to that next.

Eliminating numbers on the grid

eliminate(board, tile, digit) {
  // if the tile does not contain the digit
  // there is nothing for us to do on this tile
  if (!board[tile].includes(digit)) return board;
  
  // eliminate the number from the available values
  board[tile] = board[tile].replace(digit, '');

  // when the tile has no possible values left
  // we have reached a contradiction or unsolvable path
  if (board[tile].length === 0) return false;

  // if there is a digit on the tile
  // eliminate that number from all
  // vertical, horizontal, and same-square tiles
  if (board[tile].length === 1) {
    let result = true;
    for (const key of this.peers[tile]) {
      result = this.eliminate(board, key, board[tile]);
      if (!result) return false;
    }
  }

  // for each associated tile of the tile (itself included)
  for (const u of this.units[tile]) {
    const fieldsWithSameNum = [];

    // check if each associated field has the same number
    for (const s of u) {
      if (board[s].includes(digit)) {
        fieldsWithSameNum.push(s);
      }
      // no need to check for more if there is already more than 2
      if (fieldsWithSameNum.length > 2) break;
    }

    // reached a contradiction or unsolvable path
    if (fieldsWithSameNum.length === 0) return false;

    // if only one associated tile with the same number
    // assign that number to the tile
    if (fieldsWithSameNum.length === 1) {
      if (!this.assign(board, fieldsWithSameNum[0], digit)) {
        return false;
      }
    }
  }
  
  return true;
}

The elimination function has multiple uses. Besides eliminating the digit specified by the parameter, we also make sure to:

1. Check if the tile is empty (reach a dead end)
2. If there is only one number left eliminate that number in vertical, horizontal, and same-square tiles
3. Check if there are associated tiles with the same number, if not then place it on said tile

NOTE: The third step is important to keep going with the elimination process.

The most important aspects of the function are:

if (board[tile].length === 0) return false;

and

if (fieldsWithSameNum.length === 0) return false;

Because it tells the executing branch to stop as it has reached a dead end or unsolvable state.

Searching recursively depth first and eliminating

search(board) {
  if (!board) return null;

  let max = 1, tile = null;

  for (const s of this.squares) {
    if (board[s].length > max) {
      max = board[s].length;
      tile = s;
      break;
    }
  }

  // if every tiles length is 1, its solved and therefor return
  if (max === 1) return board;

  // recursively start creating branches that search, insert and eliminate
  for (let i = 0; i < board[tile].length; i++) {
    const res = this.search(this.assign({ ...board }, tile, board[tile][i]));
    if (res) return res;
  }

  return null;
}

The search function iterates over the board to find a tile with more than 1 possibility and recursively:

1. Insert the first possible number
2. Star an elimination cycle
3. Check if the branch is solved or not

If its solved it will return the solved board. If not, it will return null and terminate that branch then pick another branch to check. Until we reach a "solved" state.

Using it

Export the solver class and import or require it in your desired JS file to use. For example:

const Solver = require('./solver');

// you can use a string, i do this for visibility
const board = [
  '000000010',
  '000002003',
  '000400000',
  '000000500',
  '401600000',
  '007100000',
  '050000200',
  '000080040',
  '030910000'
].join('');

const solvedPuzzle = Solver.search(Solver.solve(board));

The returned solvedPuzzle will be an object (key/value pair) with the tile names as keys and the solved board as value.

Helpers to check if puzzle is correct or not

This helper class gives us two functions (convertToArray and isCorrect). convertToArray transform the object into a 2D array and isCorrect checks whether the board is solved correctly.

function convertToArray(grid) {
  const arr = Object.keys(grid)
  const tempArr = [[]];
  let tempCounter = 0;
  for (let i = 0; i < arr.length; i++) {
    if (i % 9 === 0 && i !== 0) {
      tempArr.push([]);
      tempCounter++;
    }
    tempArr[tempCounter].push(grid[arr[i]]);
  }
  return tempArr;
}


function checkHorizontally(grid, y, x, n) {
  for (let i = x; i < 9; i++) {
    if (grid[y][i] == n) {
      return false;
    }
  }
  return true;
}

function checkVertically(grid, y, x, n) {
  for (let i = y; i < 9; i++) {
    if (grid[i][x] == n) {
      return false;
    }
  }
  return true;
}

function isCorrect(grid) {
  for (let y = 0; y < grid.length; y++) {
    for (let x = 0; x < 9; x++) {
      if (!checkHorizontally(grid, y, x + 1, grid[y][x])) {
        return {isCorrect: false, y, x};
      }
      if (!checkVertically(grid, y + 1, x, grid[y][x])) {
        return {isCorrect: false, y, x};
      }
    }
  }
  return {isCorrect: true};
}

module.exports = { isCorrect, convertToArray}

Using the helpers

Convert the board to a 2D array first then check. For example:

const Solver = require('./solver');
const { convertToArray, isCorrect} = require('./checker');

// or you can use a string, i do this for visibility
const board = [
  '000000010',
  '000002003',
  '000400000',
  '000000500',
  '401600000',
  '007100000',
  '050000200',
  '000080040',
  '030910000'
].join('');

const solvedPuzzle = Solver.search(Solver.solve(board));
const isSolved = isCorrect(convertToArray(solvedPuzzle));

console.log(isSolved);

Through the result see if its solved successfully. We will be told where it went wrong if it did not solve correctly.

Conclusion

You have now made a module that can solve any sudoku puzzle, and another module that helps with conversion and checking. You can use these modules in either a node.js environment or a browser environment for whatever reason you wish.

Potential improvements

You can add a lot of potential improvements, or create neat web projects. For instance:

• Make a graphical sudoku solver in HTMl and JS
• Add all sorts of features to that graphical solver, like colors of where it saw a conflict or went wrong
• Create a webapp that creates sudoku puzzles with the solution included All that and whatever else your imagination can come up with!

Sources

All credit for the algorithm and beyond amazing mathematical explanations goes to Peter Norvig on this great article: Solving Every Sudoku Puzzle by Peter Norvig

However if you want to look at one of my own projects using this algorithm and program to make a graphical sudoku solver: the repository can be found here